Algorithm
Problem
[338.] Counting Bits
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.
Example 1:
Input: 2 Output: [0,1,1]
Example 2:
Input: 5 Output: [0,1,1,2,1,2]
Thought
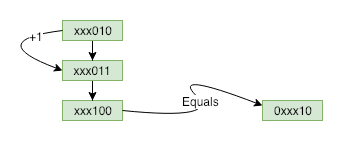
The basic idea under dynamic planning is to find the recurrence equation.
The count of 1’s in number n, written as c(n), can be calculated through checking if number n-1 is even or odd.
Following is a simple demonstration:
Solution
class Solution {
public:
vector<int> countBits(int num) {
std::vector<int> result(1, 0);
for (int i = 1; i <= num; ++i)
{
result.push_back((i % 2 == 0)?(result[i>>1]):(result[i - 1] + 1));
}
return result;
}
};
Review
This article explains Shamir’s secret sharing scheme in an easy way.
Suppose that you are given an task to design a lock-key management system. The requirements are listed as follows:
- Each of n participants has got equal part of the whole key.
- At least k participants are needed to be absent to restore the whole key.
- Lesser than k participants cannot restore the key, no matter how powerful the computer they use is.
Shamir’s (k,n) threshold scheme is designed to target this issue, and the basic idea under it is polynomial interpolation.
From reference 2, we can get that polynomial has following perfect property:
Given d + 1 pairs (x1, y1),…,(xd+1, yd+1), with all the xi distinct, there is a unique polynomial p(x) of degree (at most) d such that p(xi) = yi for i = 1,2,…,d +1.
At the middle part of this article, the author describes the principle about restoring the key through Lagrange interpolating method, using a simple polynomial function with degree of two.
Then, at the end part, the author brings in an issue caused by integer arithmetic, and also shows how to address it through modulo arithmetic.
It’s easy to understand the fundamental idea under secret sharing algorithm. And if you want to know more about it, you can refer to a note, which is attached at the end of this post.
Tip
With this tool, you can do anything you can dream up.
Following demonstrates using fpp to select possible modifications you want to add and commit.
Share
Google has been a phenomenally successful company, and one main reason of its big suscess is that Google has developed excellent software engineering practices.
The author tries to catalogue and briefly describe Google’s key softwareengineering practices.
It covers three aspects, including software management, project management, and people management.
Google has created a huge operation system to support easy software operation, including coding, debugging and releasing. It can make the programmers to focus on doing the true valuable programming things. When talking about feature releasing, Google has maintainted stagging server apart from production server. And using a gradual roll-out strategy can make sure sufficient pre-release testing.
Google uses OKR to do the target manangement. Individuals and teams at Google are required to explicitly document their goals and to assess their progress towards these goals. And they are permitted to spend up to 20% of their time working on any project of their choice, without needing approval from their manager or anyone else. It’s a free company climate, and everyone knows what he/she is expected to fulfill.
Google separates the engineering and management career progression ladders, separates the tech lead role from management, embeds research within engineering, and supports engineers with product managers, project managers, and site reliability engineers (SREs). The division of labour is clear-cut , and everyone is charged with specific responsibilities.
Reference
- https://cs.jhu.edu/~sdoshi/crypto/papers/shamirturing.pdf
- https://people.eecs.berkeley.edu/~daw/teaching/cs70-s08/notes/n10.pdf

Comments